The Art of Feature Engineering
Feature Engineering이란?
기존에 있는 데이터의 변수로 feature를 변경하거나, 새롭게 추가하여 모델링을 하거나, 예측을 할때 데이터를 더 유용하게 만드는 방법이라고 할 수 있습니다. feature engineering의 한 예를 들면, 데이터는 날짜별(date(dd-mm-yy))로 쇼핑몰에 얼마나 고객들이 방문하는지에 대한 내용을 담고 있다. 이제 이 데이터를 이용해 쇼핑몰에 고객들이 얼마나 방문하는지 예측을 할 것이다. 하지만 만약 날짜별 쇼핑몰 방문 수를 했을때, 날짜를 그대로 예측하는데 사용하면 어떻게 될까... 물론 그 날짜 그대로 사용하면 의미있는 결과는 나올 수 없다. 하지만 기존에 있는 변수를 이용해서 새로운 변수들을 생성한다면 의미있는 데이터를 추출 할 수 있다. 풀어 설명하면 2016년 6월 20일, 2016년 6월 21일 즉 일별로 방문수를 예측한다면 일정한 패턴을 찾기 어렵습니다. 하지만 기존 날짜의 값을 이용해 요일을 생성한 뒤에 처리하면 얘기는 달라집니다. 월요일에 방문하는 사람의 수와, 화요일에 방문하는 사람의 수는 확실히 예측하는데 더 좋은 결과를 줄 수 있습니다.
Feature Engineering의 처리가 무엇인가
Feature Engineering은 앞서 언급한 Variable Identification, Univariate, Bivariate Analysis, Missing Values Imputation, 그리고 Outliers Treatment의 5단계를 수행한 후에 수행을 합니다. Feature engineering은 크게 2가지 스텝으로 구분이 가능합니다.
- Variable transformation
- Variable / Feature creation
data exploration에서 위 두개의 스텝은 필수이고, modeling을 하거나 prediction을 하는데 도움을 줍니다.
Variable Transformation 이란?
데이터를 모델링하는 과정에서 함수를 통해 변수를 변형하는 것을 말합니다. 예를 들어 feature의 값이 x라고 할때, x의 값에 square / cube root또는 logarithm을 하는 것을 말합니다. 한마디로 transformation은 변수의 distribution과 다른 변수들사이에 관계를 변경하는 과정입니다. 그렇다면 언제 transformation을 하는게 유용할지 알아보도록 하겠습니다.
Variable Transformation은 언제 하는게 좋을까
아래 상황에서는 variable transformation을 하는게 필수적입니다.
변수의 스케일을 변경할때 사용을 합니다. 이 transformation은 변수의 분포에는 영향을 미치지 않기 때문에, 여러개의 데이터를 그래프로 표현한뒤에 값의 분포를 비교해 이해할때도 사용하면 좋습니다.
- non-linear의 관계를 linear 관계로 변경할때 사용합니다. linear한 관계를 갖는 변수들을 비교하는것은 쉽지만, non-linear, curve의 관계를 갖는 변수들 사이에서는 비교하는게 어렵습니다. transformation을 사용하면 non-linear 관계를 linear 관계로 변경이 가능합니다. 관계를 linear하게 변경하면 scatter plot을 사용해 쉽게 두개의 변수 사이의 관계를 확인할 수 있고, 또한 prediction의 성능을 향상시킬 수 있습니다. Log transformation이 공통적으로 사용하는 transformation 기술입니다.

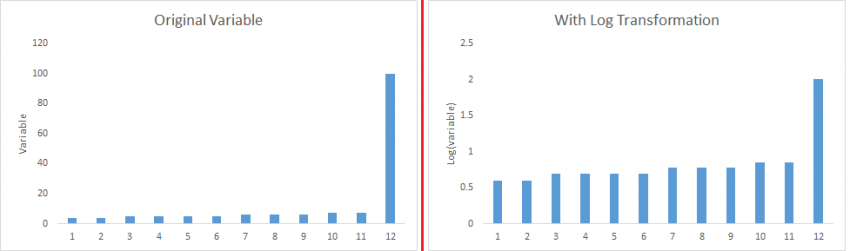
- 대칭적인(Symmetric) 분포가 skewed distribution보다 데이터를 해석하거나 추론을 쉽게 할 수 있습니다. 어떤 모델링 기술에서는 변수들의 normal distribution을 요구를 합니다. 그렇기 때문에 만약 변수가 skewed distribution을 갖고 있다면, transformation을 통해 skewness를 줄일 수 있습니다. 아래 왼쪽 그래프에서 변수에 square /cube root 또는 logarithm을 수행하면, 오른쪽 그래프와 같이 skewness가 감소한 결과를 얻을 수 있습니다.
- 사람의 관점으로 부터 transformation이 필요할때가 있습니다. 예를 들어서 연구원의 나이와 연구원의 역량의 관계를 보려고 할때, 이때 나이를 <30, 30-45, >45의 나이 그룹 버킷으로 categorizing을 한 뒤에, 각 그룹에 대해서 다른 전략을 수행하는게 올바른 방법이라고 할 수 있습니다. 이처럼 categorizing 기술을 Binning이라고 합니다.
Variable Transformation의 방법
transform variables을 하기 위한 방법은 다양합니다. 이번에 설명하는 방법은 square root, cube root, logarithmic, binning입니다. 각 방법의 장점과 단점에 대해서 알고 알맞은 경우에 사용하길 바랍니다.
- Logarithm
변수의 분포를 변경하기 위해서 사용하는 transformation 방법입니다. 이 방법은 변수들의 분포가 오른쪽으로 skweness된 것을 감소하기 위해 사용합니다. log의 특성상 0과, negative의 값은 적용이 될 수 없습니다.
- Square / Cube root
logarithm에 비해서 많이 사용되지는 않는 방법입니다. 하지만 logarithm에서 negative의 값과 0에 적용이 안되는 단점이 있습니다. 반면, cube root는 negative값과 0의 값에 적용이 가능합니다. square root는 0을 포함한 positive 값이 가능합니다.
- Binning
binning은 percentile, frequency의 기존 데이터를 categorize하기 위해서 사용됩니다. categorization 기술의 결정은 business 도메인 지식이 필요합니다. 수입을 예로 들었을때, High, Average, 그리고 Low로 나눌 수 있습니다. 또한 두 개 이상의 변수의 값에 따라 co-variate binning을 수행 할 수 있습니다.
Feature / Variable Creation 장점
Feature/variable creation은 기존 variables/features를 이용해 새로운 variables/ features를 만들어내는 과정을 말합니다. 예를들면, date(dd-mm-yy)를 입력 값으로 가지고 있을때, 기존 date의 값을 이용해 day, month, year, week, weekday의 새로운 값들을 생성할 수 있습니다. 새로운 값들은 기존에 date(dd-mm-yy)보다 관계를 찾는데 도움을 줄 수 있습니다. 위 예제에서 백화점 방문객을 예측할때도 date(dd-mm-yy)를 이용하면 관계를 찾기 어렵지만, 요일을 이용하면 관계를 보다 더 잘 찾을 수 있었던 것도 feature/variable creation의 덕분입니다.

새로운 feature를 생성하기 위한 방법은 다양하게 있습니다. creating derived variables와 creating dummy variables가 있습니다. 각각 살펴보면
- creating derived variables - 기존 변수에서 새로운 변수를 생성하는 것을 말합니다. log, binning 등 다양한 방법으로 새로운 변수를 생성할 수 있습니다.
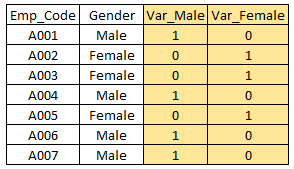
- creating dummy variables - 카테고리 데이터를 numerical 변수로 변경하는 것을 말합니다. dummy variables은 Indicator variables로 불리기도 합니다. 아래와 같이 Gender가 Male, Female의 Categorical variables일때 Male, Female의 새로운 dummy variables을 생성했습니다. 확률모델에서 Categorical variable을 predictor로 사용할때 유용합니다.
[참고]
http://www.analyticsvidhya.com/blog/2016/01/guide-data-exploration/
'Big Data > 데이터 분석' 카테고리의 다른 글
| [데이터 분석] Python 라이브러리 - Pandas, Matplotlib, Numpy 10분만에 배우기 (0) | 2021.05.03 |
|---|---|
| [데이터 분석] 머신러닝 예제 - Loan Prediction (0) | 2021.05.03 |
| [데이터 분석] Data Exploration Guide - Outlier(3) (0) | 2021.05.03 |
| [데이터 분석] Data Exploration Guide - Missing Value Treatment(2) (0) | 2021.05.03 |
| [데이터 분석] Data Exploration Guide - (1) (0) | 2021.05.03 |


